Кластерный анализ в Statistica. Часть 2. Иерархическая кластеризация

В данном посте расскажу как объединять пробы в кластеры методом иерархической кластеризации. Но подход подойдет и для выделения ассоциаций переменных. Метод не относится к статистическим методам. Чистая математика. Берем меру расстояния между объектами, и выбираем метод объединения. Все объекты объединяются шаг за шагом пока не будет один кластер. Так что надо решить на каком шаге выделить кластеры.

В каждом новом посте я использую приемы форматирования и редактирования, которые обсуждал в предыдущих постах. Например, как импортировать данные из Excel в Statistica, как добавить переменную, и др. Так что читайте или задавайте вопросы.

Рис. 1. Импортируем данные и присваиваем имена каждой пробы из столбца ID (v1). У меня номера проб текстовые, не числовые.

Рис. 2. Для кластерного анализа необходимо стандартизовать данные. Стандартизация – это когда берется все наблюдения по определенному хим. элементу, из каждого наблюдения вычитается среднее значение в столбце и разница делится на стандартное отклонение. Зачем это нужно? Дело в том, что одни перменные имеют очень высокие содержания (например, сотни грамм на тонну), а другие ультранизкие (микрограммы на тонну). Соответственно первые имеют “высокий вес”. Но нам важны все в относительном порядке. Поэтому процедура стандартизации их уравнивает. Кстати, для кластерного анализа не нужно определять тип распределения и подгонять данные. Это по желанию.

 

Рис. 3. Выбираем переменные и щелкаем ОК. Исходные данные станут стандартизированными. Каждое наблюдение будет иметь значение стандартного отклонения и распределено относительно нуля.

Рис. 4. Выбираем вкладку Statistics – Mult/Exploratory – Cluster.

На заметку. В Статистике есть два вида анализов: подтверждающий и разведочный. Разведочный – когда ищем закономерности в данных, а подтверждающий когда их применяем для анализа. Некоторые методы могут быть одновременно и разведочными и подтверждающими. Например, дискриминантный метод и ищет почему известные группы разделяются, и дает постериорное разделение наблюдений по группам по уже найденным закономерностям. Так кластерные анализы тоже могут быть и теми и другими. Иерархическая кластеризация – разведочный метод.

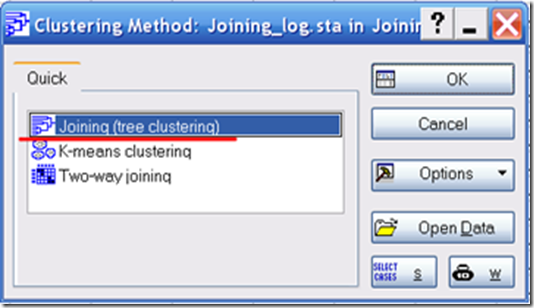Рис. 5. Выбираем метод Объедиенения (Иерархической кластеризации, Joining). Другие методы рассмотрим позже. Каждая проба сама по себе является кластером, и мы их (пробы) пошагово объединяем пока не будет один кластер – вся выборка. Как вы можете догадаться, можно не объединять пошагово, а разделять из одной выборки в маленькие. Да, но в Statistica такой метод не реализован.

Рис. 6. Открываем вкладку Расширенные настройки (Advanced).

Input file: raw data - Входные данные: сырые данные. Другой выбор – корреляционная матрица. Но об этом в следующий раз.

Cluster: Cases (rows) – Кластеризовать: Наблюдения (строки). Еще можно найти группы переменных.

Amalgamation (linkage) rule: Ward’s method – Правило объединения: метод Варда. Данный метод пытается минимизировать дисперсию в выбранных группах. Поэтому он старается создать маленькие кластеры. Метод дает интересные результаты, поэтому часто используется. Выбор правила объединения стоит за исследователем. Поэтому просто постарайтесь представить какие у вас кластеры. Например, они они имеют разный размер (редкие аномальные объеты на неоднородном фоне), то можно попробовать взвешенный центроидный метод (Weighted centroid method (Median)).  В нем расстояния между кластерами вычисляется как геометрическое расстояние между центрами тяжести с учетом весов (по размерам кластеров). Центр тяжести – координата соответствующая медианам всех наблюдений. То есть выбросы для него несущественны. Пробуйте разные методы и сравнивайте. Как поговаривают геохимики “Настоящую аномалию закопать невозможно”.

Distance measure: Euclidean distances – Мера расстояния: Эвклидово расстояние. Мера расстояния – краеугольный камень кластерного анализа.  Тема не на один пузырь и одну докторскую. Собственно, в кластерном анализе мы измеряем расстояние между пробами (и кластерами) с помощью некоторой его меры. Эвклидово расстояние – это кратчайшее геометрическое расстояние. Помните про гиппотенузу и катеты: “Пифагововы штаны на все стороны равны, а квадрат гиппотенузы равен сумме квадратов катетов”?. Это полезно когда кластеры имеют форму шаров.

Если кластеры сильно вытянуты, то необходимо использовать расстояния Махаланобиса. К сожалению, они тут не реализованы. Но можно попробовать метод Single Linkage (Объединение ближайших соседей).

Так же, для геохимии вполне подойдут Расстояния Манхэтанна (не чувстивтельно к выборосам), и Квадрат Евклидово Расстояния (усливает расстоние между кластерами путем возведения в квадрат).

Выбор сделан, щелкаем ОК.

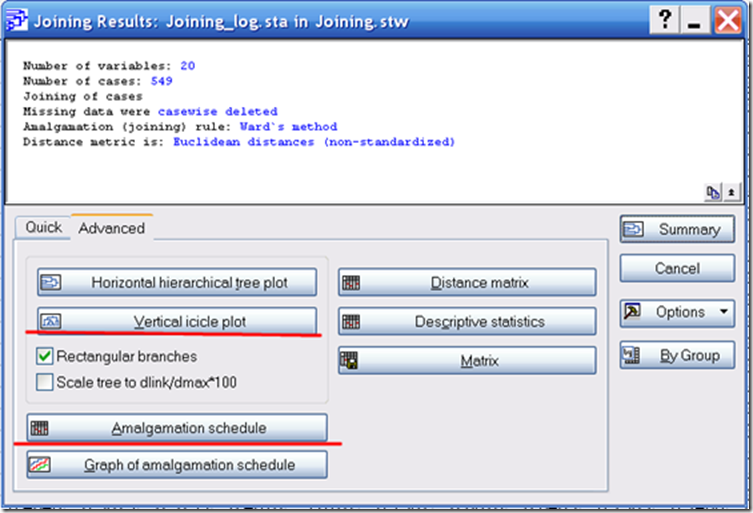Рис. 7. Переходим во вкладку Расширенное (Advanced). Сначала строим график объединения проб Vertical icicle plot, а потом выведем его табличный аналог – Amalgamation Shedule.

Рис. 8. Вертикальная дендрограмма кластеризации.

Смотрим на данный график как на кисть винограда. Выделяем крупные кисти в объеме до 4-5 штук. Это и будут наши кластеры. Помните про стадийный подход и принципы системного анализа: выделяем обобщенные кластеры, а потом уточняем интересующий кластер отдельно.

  Рис. 9. Тот же график. Только я тут убрал заголовки, подписи. Изменил максимальное значение расстояния на 200. Собственно, выделяются три крупных кластера. Причем два соединяются.

Рис. 10. Передумал и решил сделать шесть кластеров.

Рис. 11. Рисуем красные прямоугольники и дважды щелкаем на них. Задаем динамическое изменение масштаба.

Красные прямоугольники рисуем, что бы было удобнее потом масштабировать график на определнном кластере. Это нужно, что бы навести мышкой на границу объединения и получить более точное значение уровня на котором произошло объединение субкластеров.

Рис. 12. Масштабируем график на первом кластере. Навелем мышкой на горизонтальную линию, которая из сединяет. Значение приблизительно 25,9. Тут надо деликатно делать. Часто эти значения близки. И если сомневаеетесь, то еще масштабируйте график.

Рис. 13.Открываем таблицу объединения (Amalgamation Shedule). В самом левом столбце показаны определенные уровни на которых произошло объединение конкретных кластеров. Я решил выделить шесть кластеров. На рис. 12 первый кластер был объединен на уровне приблизительно 25,9. Найдем его.

Кстати, у меня использована относительно небольшая выборка 549 проб. При использовании тысяч проб, будет затруднительно работать. Не расслабляйтесь.

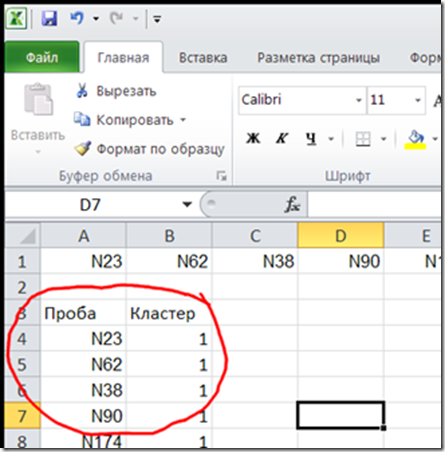
Рис. 14. Находим первый кластер. Уровень 25,97356. Выделяем строку. В ней перечислены все пробы из кластера. Строку копируем и вставляем в Excel. А что? Удобная программа.

 

Рис. 15. Копируем строку и….

Рис. 16. Вставляем с транспонированием. Для этого на ячейке щелкаем правой клавищей и выбираем “Специальная вставка”.

 

Рис. 17. Получили. Назвачаем пробам первый кластер.

Повторяем все с остальными кластерами. Далее в Statistica и Excel соритруем данные по столбцу номера пробы. И добавляем столбец с кластерами из Excel в Statistica. Немного муторно, но работает.

Скажу сразу. Я эту работу делал в два этапа и объединил результаты. Поэтому  у меня шесть кластеров с номерами от 0 до 5.

Рис. 18.

Рис. 19. Теперь у проб есть группирующая переменная “Кластер”. Определим, чем же они отличаются. Для этого построим графики типа Ящик-с-усами для всех переменных.

Как строить данные графики смотрите предыдущие посты.

Если взглянуть на рис 9 и 10, то увидим, что кластеры 0 и 1 объединяются в один более крупный кластер, тоже с остальными кластерами.

1. Кластеры 0, и 3 скорее всего соответствуют рудной минерализации. Потому что у них повышенно содеражние рудных компонентов;
2. Кластер 1 совождает кластер 0, а кластер 2 сопровождает кластер 3;
3. Кластер 5 – имеет фоновые содержания по всем компонентам. А кластер 4 – соотствует выносу элементов;
4. Кластер 5 можно использовать в качестве подвыборки фоновых проб для определения различий распределения хим. элементов в зависимости от ландшафта. Только надо взять пробы, которые удалены от явных аномалий. Поскольку это нормально, когда часть фоновых проб попадают в контур аномалии.

Рис. 20. Построим график распределения кластеров в пространстве.

Рис. 21. График распределения кластеров в пространстве.

На севере концентрируется кластеры 0 и 1, они окружены кластером 2. Кластер 2 все таки ближе к 0 и 1, чем к 3-му. В центре расположен кластер 3, он так же соседствует с кластером 2.

Рис. 22. Построим график опять, но выделим лишь более интересные кластеры 0, 1, 2, которые предположительно соответствуют рудной минерализации. Самые высокие содержания  имеет кластер 0. В кластере 1 меньше, и еще меньше в кластере 2. Зональность – хорошее качество.

Вообще я бы не стал говорить “Бурить тут!”, а дал бы рекомендации к заверке аномалии поисковыми маршрутами, детализации геохимическими методами и изучению с помощью геофизических методов.

Рекомендую прочитать:

1. Буреева  Н.Н.  Многомерный  статистический  анализ  с  использованием  ППП “STATISTICA”. Учебно-методический материал по программе повышения квалификации «Применение программных средств в научных исследованиях и преподавании математики и механики». Нижний Новгород, 2007, 112 с.;
2. Дэвис Дж. С. Статистической анализ данных в геологии: Пер. с англ. В 2 кн./Пер. В.А. Голубевой; Под. ред. Д.А. Родионова. Кн. 1. – М.: Недра, 1990. – 319 с.: ил. ISBN 5-247-02122-3;
3. В.П. Боровиков Популярное введение в программу STATISTICA.

(к сожалению ссылки лучше у меня не осталось)

Удачи!

PS. Части 1 еще нет.